ON THE ART AND SCIENCE OF ACOUSTIC INSTRUMENTS
© 2000–2025 Cris Forster
CHAPTER 11: WORLD TUNINGS
Part III: Indian Music
South India
Section 11.32
An imaginary east-to-west diagonal from Calcutta, near the Bay of Bengal, to Mumbai (Bombay), on the coast of the Arabian Sea, roughly divides the subcontinent of India into two geographical and cultural areas called North India and South India. The former region is known for Hindustani music, and the latter, for Carnatic music. Although both cultures evolved from the same ancient tradition, by the 17th century each had developed a separate musical vocabulary and unique styles in the performance of ragas.
Before we discuss these two traditions, let us first address the question, “What is a raga?” The answer is extremely complex because ragas are musical expressions that continuously change in time. Most ragas consist of two basic elements: (1) a set of technical definitions and instructions, transformed into music through (2) spontaneously improvised performances.[1] Because Indian music is inherently melodic in nature, musicians have created literally thousands of different ragas. In the 16th and 17th centuries, theorists attempted to organize this incomprehensible plethora of ragas by creating organizational systems based on mathematically defined tunings and combinatorics. However, because such efforts compelled theorists and musicians to closely examine the quintessential relation between the technical and musical aspects of ragas, these systems profoundly influenced not only intellectual definitions of ragas, but artistic interpretations as well.
In the next five sections, we will examine the evolution of South Indian ragas in the writings of Ramamatya (fl. c. 1550), Venkatamakhi (fl. c. 1620), and Govinda (c. 1800). These three writers focused on a theme common to all organizational systems, namely, the principle of abstraction. Ramamatya was the first Indian theorist to formulate a system based on a mathematically determined tuning. He defined (1) a theoretical 14-tone scale, (2) a practical 12-tone tuning, and (3) a distinction between abstract mela ragas and musical janya ragas. He then combined these three concepts to identify 20 mela ragas, under which he classified more than 60 janya ragas. Venkatamakhi extended Ramamatya’s approach, and proposed a system that consists of 72 heptatonic permutations called melakartas. He then identified 19 melakartas, which he used to classify dozens of janya ragas. Finally, Govinda extended Venkatamakhi’s basic concept, and defined the present-day system, which consists of 72 modern mela ragas, or 72 theoretically constructed heptatonic scales.
We may think of these developments as representing three interrelated stages in the history of South Indian music. Ramamatya, Venkatamakhi, and Govinda created organizational systems based on the principle of musical abstraction, combinatorial abstraction, and theoretical abstraction, respectively. As such, these underlying principles do not tell us how to understand the resulting systems. Therefore, consider the following three interpretations. In the writings of Ramamatya and Venkatamakhi, the terms mela ragas and melakartas, respectively, refer to prototypes — or collections of seven tones — that function as abstract raga-categories. In the 16th, 17th, and 18th centuries, theorists and musicians used melas for only one purpose: to organize and classify musical ragas. Consequently, in the original sense, melas never represented regular scales, or musical ragas. Figure 11.30 shows two melas identified by Ramamatya enclosed in separate circles to convey the impression of pools of seven tones that similar musical janya ragas have in common. In most texts, melas are represented as linear sequences of notes on a treble staff. Westerners, when presented with progressions of notes in regular ascending and/or descending order, unwittingly interpret such sequences as scales. Because this tendency seriously interferes with a historical understanding of South Indian music, I have chosen to equate the original melas with the terms raga-categories, prototypes, and tone pools.
This definition of mela also applies to Venkatamakhi’s 72 melakartas in Figure 11.32. Here too, the reader should not confuse sequential progressions of tones in the lower and upper tetrachords with scales or ragas. If I had chosen to ignore the logical and mathematical sequences of tones required to generate this twelve-by-six array, then Venkatamakhi’s combinatorics would be completely incomprehensible. In the final analysis, Venkatamakhi’s melakartas also function as abstract raga-categories, prototypes, or tone pools.
Finally, in Govinda’s text, the term mela ragas does mean scales — or heptatonic sequences of tones in regular order — which he used to identify (1) 72 abstract raga-categories or prototypes, and (2) a new class of 72 musical mela ragas. Here, for the first time in the history of Indian music, the theoretical concept of a symmetric scale has a musical function. (Therefore, while we may consider Govinda’s mela ragas as prototypes, we should not think of them as tone pools.) By definition, all mela ragas must consist of seven straight ascending and seven straight descending tones, and a given mela raga as musical raga must include all seven tones in at least one krama (lit. straight) or vakra (lit. crooked, or zigzag) ascending and descending sequence. As discussed in Section 11.38, modern writers have deplored the latter development because theoretically constructed scales tend to obliterate unique technical and musical characteristics for which musical ragas are known. Such oversimplifications, they argue, lead to mechanized and homogenized musical performances.
Section 11.33
Approximately three hundred years after Sarngadeva’s Sangitaratnakara — an encyclopedic work used by musicians to this day — Ramamatya wrote a short work in 1550 entitled Svaramelakalanidhi. In this 25-page treatise, Ramamatya revolutionized the theory and practice of music not only in South India, but in North India as well. Near the beginning of the treatise, Ramamatya explains his motivations for writing the Svaramelakalanidhi, and thereby demonstrates that he was fully aware of the intellectual and musical challenges of his time:
Sva. 1.24 — The Science of Music has, both in theory and practice, degenerated into conflicting views. Let [me] reconcile . . . all (the conflicting views) and write a (new) science.[2] (Bold italics and text in brackets mine.)
Later writers and theorists followed Ramamatya’s lead regarding these three incipient contributions:
(1) Ramamatya defined a theoretical 14-tone scale, which he realized as a 12-tone tuning.
(2) He specified this tuning by describing the location of six frets on his vina.
(3) Based on this 12-tone scale and tuning, Ramamatya defined 20 mela ragas and used them to classify over 60 janya ragas.
In South India, Venkatamakhi theoretically resolved the mela issue seventy years after the publication of the Svaramelakalanidhi, but in North India, the classification of ragas according to thats remains steeped in controversy to this day. The first theorist who attempted to expand the traditional 7-tone scale was Sarngadeva. In a well-known passage,[3] Sarngadeva defined twelve vikrta svaras (modified notes), which he assigned to locations on or between the positions held by the suddha svaras (pure notes) in the traditional Sa–Ri–Ga–Ma–Pa–Dha–Ni–Sa1 sequence. Unfortunately, Sarngadeva’s idea remained obscure because he did not address two key difficulties. (1) He neglected to observe that five of these twelve vikrta svaras are enharmonically equivalent and, therefore, musically identical; this lack of precision probably confused later generations of readers. (2) He did not offer a tuning example by which musicians could test his theory. In contrast, Ramamatya not only fully comprehended the first problem, but also dispelled the second by giving a verifiable demonstration on his fretted vina.
Due to the historical significance of the Svaramelakalanidhi, let us first review Ramamatya’s description of the Sadjagrama:
Sva. 2.27–30 — The Svaras arise from the Srutis in such a manner that Sadja takes the fourth Sruti of the Vina; Rsabha, the seventh; Gandhara, the ninth; Madhyama, the thirteenth; Pañcama, the seventeenth; Dhaivata, the twentieth; and Nisada, the twenty-second.[4]
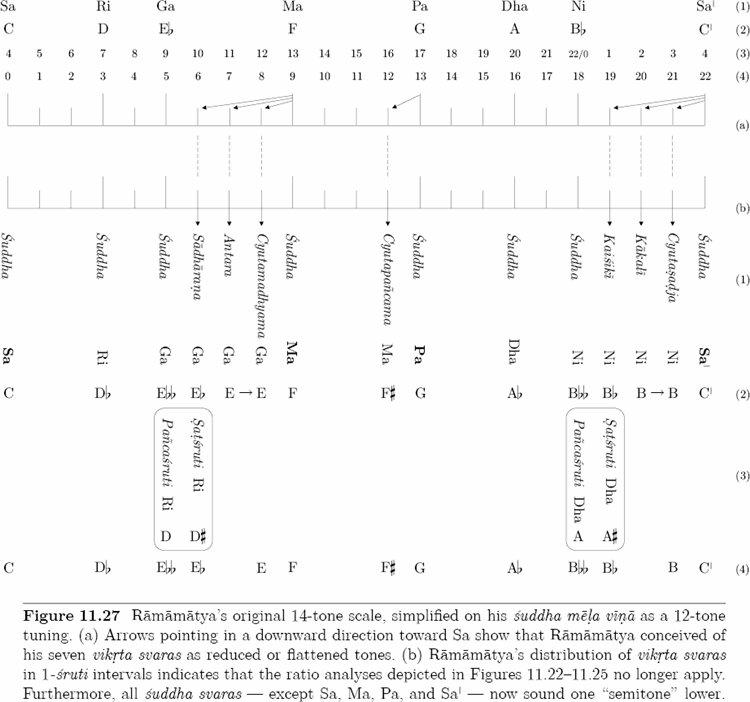
Refer to Figure 11.27(a), Rows 1 and 2, which show the familiar seven ancient suddha svaras and their modern counterparts, respectively. In Svaramelakalanidhi 5.17, Ramamatya states, “All . . . Ragas are those of the Sadjagrama,”[5] which tells us that by the 16th century, the Madhyamagrama, and with it, the concept of grama origins were considered obsolete relics of the past. (See Section 11.35.) Now, Figure 11.27(a), Row 3, illustrates the sruti distributions of the suddha svaras as described by Ramamatya. Many Indian theorists prefer to number the Sa-grama by starting on Ni, or four srutis before (below) Sa. However, because Ni never functions as a first degree or tonic of the Sa-grama, this distribution has no effect on the traditional locations of the ancient suddha svaras as enumerated in Figure 11.27(a), Row 4. In the following passage, Ramamatya confirms this point beyond doubt, establishes the existence of seven suddha svaras and seven symmetric vikrta svaras, and concludes with his critique of Sarngadeva’s twelve vikrta svaras:
Sva. 2.32–33 — These seven Svaras, beginning with Sadja, are called Suddha Svaras. While, the Vikrta Svaras are also seven. In all, there are fourteen Svaras — Suddha and Vikrta.
33–34 — How is it that . . . only seven Vikrta Svaras [are given here], while Sarngadeva mentioned, in his Sangitaratnakara, so many as twelve?
34–38 — It is true that, from the theoretical point of view, the number twelve may be desirable. But, in actual practice, there are only seven Vikrta Svaras, as being different from the seven Suddha Svaras.[6] (Bold italics mine.)
Ramamatya then accounts for the five enharmonic equivalents in Sarngadeva’s text, and continues by giving the definitions of his own seven vikrta svaras:
Sva. 2.44–49 — ‘Cyutasadja’ is the name given to that Sadja which gives up its own fourth Sruti and takes the third one. The same rule equally applies to ‘Cyutamadhyama’ and ‘Cyutapañcama’. When Suddha Madhyama takes the first Gandhara Sruti, it is called ‘Sadharana Gandhara’; but when the same Suddha Madhyama takes the second Gandhara Sruti, it goes by the name of ‘Antara Gandhara’. When, again, Suddha Sadja takes the first Nisada Sruti, it is called by expert musicians ‘Kaisiki Nisada’; but when it takes the second Nisada Sruti, it goes by the name of ‘Kakali Nisada’. Thus, the seven (Vikrta Svaras) have been described.[7]
(The prefix cyuta means lowered, and the modern term sadharana means common, or ordinary.) According to this text, all seven vikrta svaras are defined by three different sruti reductions of Sa and Ma, and a 1-sruti reduction of Pa. Arrows in Figure 11.27(a) illustrate Ramamatya’s tendency to define the vikrta svaras as lowered tones, and the vertical dashed lines that lead to Figure 11.27(b) indicate the locations of the vikrta svaras on his 22-sruti scale. However, because in North and South Indian music the Sa–Pa interval represents ratio 3/2 — or an immutable consonance — Ramamatya associates Cyutasadja with Ni and calls it ‘Cyutasadja Ni’, and associates Cyutapañcama with Ma and calls it ‘Cyutapañcama Ma’. As indicated in Figure 11.27(b), Rows 1 and 2, Ramamatya assigns seven alternate names to the following suddha and vikrta svaras:
Sva. 2.49–57 — . . . [1] On account of its identity with Nisada, Cyutasadja is also called Cyutasadja Ni. [2] On account of its identity with Gandhara, Cyutamadhyama is also called by me Cyutamadhyama Ga. [3] On account of its identity with Madhyama, Cyutapañcama is also called by me Cyutapañcama Ma. . . . [4] Suddha Gandhara [Ebb] is called by me Pañcasruti Ri [D]. . . . [5] Sadharana Gandhara [Eb] is, in practice, also called Satsruti Ri [D#]. [6] Likewise . . . Suddha Nisada [Bbb] is called Pañcasruti Dha [A]; [and] . . . [7] Kaisiki Nisada [Bb] is called Satsruti Dha [A#].[8] (Numbers and text in brackets mine.)
(Pañcasruti defines a 5-sruti interval above Sa or Pa, and satsruti, a 6-sruti interval above Sa or Pa.) As indicated in Figure 11.27(b), Row 3, the latter four enharmonic equivalents — D, D#, A, A# — are absolutely vital to South Indian music because they enable theorists and musicians to describe chromatic intervals without notating two consecutive svaras of the same name. For example, in his definition of Sri-raga (see Section 11.35), Ramamatya correctly describes the first chromatic step as a Pañcasruti Ri [D]–Sadharana Ga [Eb] interval; although he could have described it as a Suddha Ga [Ebb]–Sadharana Ga [Eb] interval, this notation is incorrect because it utilizes two consecutive Ga’s.
In Section 11.34, we will examine the tuning of Ramamatya’s vina. This discussion will show that the ratio analyses depicted in Figures 11.22–11.25 no longer apply to Figure 11.27. Note that Ramamatya distributed his vikrta svaras in 1-sruti intervals, a division strictly avoided in all ancient texts. Furthermore, a comparison between Figure 11.27(a), Row 2, and Figure 11.27(b), Row 2, reveals that all suddha svaras — except Sa, Ma, Pa, and Sa1 — now sound one “semitone” lower. Consequently, former Suddha Ri [D] sounds Db, former Suddha Ga [Eb] sounds Ebb, former Suddha Dha [A] sounds Ab, and former Suddha Ni [Bb] sounds Bbb. Finally, with respect to Figure 11.27(b), Row 4, Ramamatya made a deliberate decision not to include frets for Antara Ga [E] and Kakali Ni [B], and thereby tuned a 12-tone scale on his vina.
Section 11.34
During the second half of the first millennium A.D., ancient harp-vinas were gradually replaced by stick-zithers, initially called alapini vinas. The latter instruments had only one string. However, in later centuries they were built with two and three strings. When compared to harp-vinas, zither-vinas have two distinguishing features. (1) All playing strings are identical in length. (2) Although the alapini vina from the 7th century A.D. did not have frets, by the 13th century, the kinnari vina had 12 to 14 frets.[9] Ramamatya’s suddha mela vina, presumably built to demonstrate the feasibility of his 12-tone scale, had four open strings tuned to anumandra (very low) Sa, ratio 1/1 [C], anumandra Pa, ratio 3/2 [G], mandra (low) Sa, ratio 2/1 [C1], and mandra Ma, ratio 8/3 [F1]. Because Ramamatya’s tuning description does not refer to “octave” equivalents, the following text includes bracketed notes with primes [1] to indicate pitches that sound one “octave” higher. We will go on to discuss the enharmonic conflict between C#/Db and F#/Gb found below.
Sva. 3.26–31 — . . . On the first Anumandra Sa-wire [C], should be placed frets Nos. 1, 2, 3, 4, 5, 6, so that they may produce respectively the following Svaras: Suddha Ri [Db], Suddha Ga [Ebb], Sadharana Ga [Eb], Cyutamadhyama Ga [E], Suddha Ma [F], and Cyutapañcama Ma [F#].
31–34 — We shall consider what Svaras these six frets produce on the other three (upper) wires. On the second wire, called Anumandra Pañcama [G], the same six frets produce respectively the following Svaras: Suddha Dha [Ab], Suddha Ni [Bbb], Kaisiki Ni [Bb], Cyutasadja Ni [B], Suddha Sa [C1], and Suddha Ri [not Db1, but C#1].
35–36 — The two Svaras, namely, Suddha Sa [C1] and Suddha Ri [C#1] produced on the second wire, occur again on the third wire . . . and are therefore of no use on the second wire.
37–39 — The Svaras, which the same six frets produce on the third Mandra Sa-wire [C1], are, as in the case of the Anumandra Sa-wire, as follows: Suddha Ri [Db1], Suddha Ga [Ebb1], Sadharana Ga [Eb1], Cyutamadhyama Ga [E1], Suddha Ma [F1], and Cyutapañcama Ma [F#1].
39–40 — Since Suddha Ma [F1] and Cyutapañcama Ma [F#1], occur again on the fourth wire, they are of no use on the third wire.
41–43 — The Svaras, which the same six frets produce on the fourth Mandra Ma-wire [F1], are: Cyutapañcama Ma [not F#1, but Gb1], Suddha Pa [G1], Suddha Dha [Ab1], Suddha Ni [Bbb1], Kaisiki Ni [Bb1], and Cyutasadja Ni [B1].[10] (Bold italics and text in brackets mine.)
Since there is no historical evidence that an Indian mathematician in c. A.D. 1550 calculated the 12th root of 2 (i.e., before Chu Tsai-yü in 1584, and before Simon Stevin in 1585; see Section 11.20), we will assume that Ramamatya described a just intoned tuning. This conclusion is also supported in Svaramelakalanidhi 3.35–36 and 3.39–40. Before we discuss these two passages, refer to Figure 11.28, which shows his fret design and gives a ratio analysis of the text. The six steps below describe how Ramamatya determined the locations of his six frets.
(1) Locate String IV, Fret 2 [G1] to sound an “octave” above Open String II [G].
(2) Locate String IV, Fret 4 [Bbb1] to sound an “octave” above String II, Fret 2 [Bbb].
(3) Locate String IV, Fret 6 [B1] to sound an “octave” above String II, Fret 4 [B].
(4) Locate String II, Fret 5 [C1] to sound an “octave” above Open String I [C].
(5) Locate String II, Fret 3 [Bb] to sound an “octave” below String IV, Fret 5 Bb1].
(6) Locate String II, Fret 1 [Ab] to sound an “octave” below String IV, Fret 3 [Ab1].
In the following passage, Ramamatya confirms this basic approach to fretting the vina:
Sva. 3.44–62 — . . . Inasmuch as the . . . Suddha Ni [Bbb], produced on the second wire by the second fret, is of the same value as the Suddha Ni [Bbb1], produced on the fourth wire by the fourth fret . . . Inasmuch, again as the . . . Cyutasadja Ni [B], produced on the second wire by the fourth fret, is of the same value as the . . . Cyutasadja Ni [B1], produced on the fourth wire by the sixth fret . . . Inasmuch, again, as the . . . Kaisiki Ni [Bb1], produced on the fourth wire by the fifth fret, is of the same value as the . . . Kaisiki Ni [Bb], produced on the second wire by the third fret . . . Inasmuch, further again, as the . . . Suddha Dha [Ab1], produced on the fourth wire by the third fret, is of the same value as the . . . Suddha Dha [Ab], produced on the second wire by the first fret; all the Svaras have been shown to be of definitely determined values. In this manner Ramamatya determined the values of all the Svaras produced on all the four wires by all the six frets.[11]
Finally, given Ramamatya’s fret descriptions and instructions in Svaramelakalanidhi 3.26–62, and his open strings tuned to the following ratios: Sa–1/1, Pa–3/2, Sa1–2/1, Ma1–8/3 [4/3], Figure 11.28 shows the only possible mathematical interpretation of this scale.

Consider now the two passages in question. In Svaramelakalanidhi 3.35–36, Ramamatya’s first observation that C1 on String II, Fret 5 sounds the same tone as Open String III is true, but his second observation that C#1 on String II (Fret 6) sounds the same tone as Db1 on String III (Fret 1) is not true. Similarly, in Svaramelakalanidhi 3.39–40, Ramamatya’s first observation that F1 on String III, Fret 5 sounds the same tone as Open String IV is true, but his second observation that F#1 on String III (Fret 6) sounds the same tone as Gb1 on String IV (Fret 1) is also not true. In both cases, Ramamatya insists that because the first observations are true, the second observations are by association also true. Indeed, if this were a 12-tone equal tempered tuning, the second observations would be true, but would not require comment. In other words, Ramamatya is forcing the issue and avoiding an inevitable encounter with the comma of Pythagoras.[12] To understand why the second observation in Svaramelakalanidhi 3.35–36 is untrue, refer to Figure 11.29(a). Here a pattern of horizontal arrows that begins on String IV, Fret 2 indicates a descending sequence of “fourths,” ratio 4/3. Now, if we simplify “octave” equivalents,[13] or if we ignore changes in register indicated by the diagonal arrows, then this sequence of descending 4/3’s emerges:
↓ 3/2 [G], 9/8 [D], 27/16 [A], 81/64 [E], 243/128 [B], 729/512 [F#], 2187/2048 [C#] (A)
Similarly, in Figure 11.29(b) a pattern of horizontal arrows that begins on String II, Fret 5 indicates an ascending sequence of “fourths.” Again, if we simplify “octave” equivalents, then this sequence of ascending 4/3’s emerges:
↑ 2/1 [C], 4/3 [F], 16/9 [Bb], 32/27 [Eb], 128/81 [Ab], 256/243 [Db], 1024/729 [Gb] (B)
Observe carefully that if we begin on 3/2 [G], then after six descending 4/3’s, Sequence A generates 2187/2048 [C#], or the apotome [see Sections 10.15 and 10.18, and Figure 16(a)]; and if we begin on 2/1 [C], then after five ascending 4/3’s, Sequence B generates 256/243 [Db], or the limma [see Sections 10.10, 10.15, 10.18, and Figure 16(b)]. These two tones are not identical; the former is a comma of Pythagoras sharper than the latter: 2187/2048 ÷ 256/243 = 2187/2048 × 243/256 = 531441/524288. We also encounter the same discrepancy in the second observation of Svaramelakalanidhi 3.39–40. After five descending 4/3’s, Sequence A produces 729/512 [F#], whereas after six ascending 4/3’s, Sequence B produces 1024/729. [Gb]. Divide the former by the latter, and find once again the comma of Pythagoras: 729/512 ÷ 1024/729 = 729/512 × 729/1024 = 531441/524288.

Note that there are two Db’s and one C# on the vina. In Svaramelakalanidhi 3.35–36, Ramamatya eliminates C#1, ratio 2187/2048 on String II, Fret 6. This is a consistent choice because the two remaining Db’s — ratio 256/243 on String I, Fret 1 and String III, Fret 1 — represent two identical “semitones.” However, observe there are also two F#’s and one Gb. In Svaramelakalanidhi 3.39–40, Ramamatya eliminates F#1, ratio 729/512 on String III, Fret 6. This is an inconsistent choice because F#, ratio 729/512 on String I, Fret 6, and Gb1, ratio 1024/729. on String IV, Fret 1, represent two different “tritones.” Two different “tritones” means two different “octaves,” “fifths,” “fourths,” etc., exist in the scale. For example, the interval between Gb1 on String IV, Fret 1, and Db1 on String III, Fret 1, is a “just fourth”: 1024/729 ÷ 256/243 = 4/3 = 498.0 ¢, but the interval between F# on String I, Fret 6, and Db on String I, Fret 1, is a “sharp fourth” that is a comma of Pythagoras [23.5 ¢] higher: 729/512 ÷ 256/243 = 144209/106701 = 521.5 ¢.
The latter choice indicates that Ramamatya did not mathematically define the svara ratios of his vina, which means that he did not base his scale and tuning theory on formal length ratio calculations. Nevertheless, because Ramamatya’s description of fret locations admits only one possible realization, we may consider his work a significant expression of musical mathematics.
With respect to the disparities between the theoretical 14-tone scale in Figure 11.27 and the practical 12-tone tuning in Figure 11.28, Ramamatya explains the elimination of Antara Ga and Kakali Ni as follows:
Sva. 3.64–72 — While all the hitherto-discussed Svaras have been fourteen in number, the theory of twelve Svaras will now be explained, without any confusion. First, the question as to why a couple of frets was not fixed to produce Kakali Ni and Antara Ga may be taken up. If two frets were fixed to produce Kakali Ni and Antara Ga, the resulting sound is a disagreeable beat; and hence the absence of the two frets to produce those two Svaras. How then can they be otherwise produced? The learned musicians are of opinion that Kakali Ni can be produced, in a way, even by the Cyutamadhyama Ga-fret. In fact, all the Ragas, in which Kakali Ni and Antara Ga play any part, may likewise be sung. Some practical musicians consider Cyutamadhyama Ga and Cyutasadja Ni as the representatives respectively of Antara Ga and Kakali Ni, on account of the very small difference in sound between them.[14] (Bold italics mine.)
Let us assume that the “disagreeable beat” occurred when Ramamatya tuned Antara Ga to a 5-limit “major third,” ratio 5/4, and Kakali Ni to a 5-limit “major seventh,” ratio 15/8. This would produce the following interval between Cyutamadhyama Ga and Antara Ga: 81/64 ÷ 5/4 = 81/80 = 21.5 ¢, and between Cyutasadja Ni and Kakali Ni: 243/128 ÷ 15/8 = 81/80 = 21.5 ¢. In both cases, the discrepancy is called the comma of Didymus, which is 2.0 ¢ less than the comma of Pythagoras. Since most musicians are unable to aurally distinguish between these two extremely similar commas, we find Ramamatya’s interpretations perfectly consistent. On the one hand, he dismisses the Pythagorean comma between C#/Db and F#/Gb, and on the other hand, he eliminates the Didymic comma between two different kinds of E’s and B’s.[15]
Table 11.16 gives the ancient length ratios of Ramamatya’s 12-tone suddha mela vina tuning, their cent values, plus four alternate note names. Turn to Figure 10.16(a) and 10.16(b), and note that this scale consists of six ascending 3/2’s, five descending 3/2’s, and an “octave.” Consequently, Table 11.16 gives the “tritone” as F#, ratio 729/512, not only because this tone represents a consistent choice, but also because the note name Cyutapañcama Ma clearly refers to a variant of F. If we were to interpret the “tritone” as Gb, ratio 1024/729, its note name would have to refer to a variant of Pa.
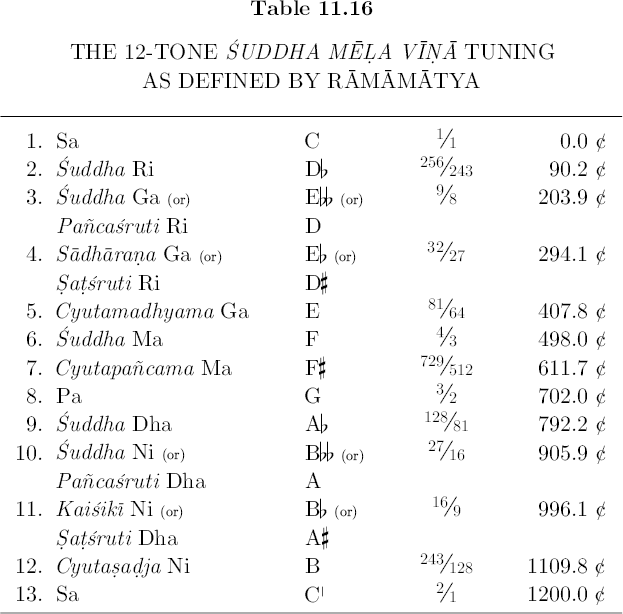
Finally, unless Ramamatya knew less than Bharata, Narada, Matanga, and Sarngadeva about the art of tuning musical instruments — a highly unlikely possibility — all these difficulties associated with commas prove two points. (1) The notion that musicians in ancient India tuned a 22-tone equal tempered scale has no basis in fact. Mathematicians and theorists design equal tempered tunings for only one reason: to disperse various kinds of commas.[16] (2) The 22-sruti scale provided an intellectual framework for the conceptualization and actualization of 5-tone, 6-tone, 7-tone, and 12-tone scales, but never 22-tone scales. Theorists who have the mathematical knowledge needed to construct sophisticated tempered or just 22-tone scales, also demonstrate awareness and mastery over the intonational difficulties presented by commas. Ramamatya’s treatise constitutes a critical step in the evolution of Indian music because he was the first writer to wrestle with these complex problems not as a mathematician, but as an inventive and visionary musician.
Section 11.35
The theoretical 14-tone scale and the practical 12-tone tuning provided Ramamatya with two prerequisite tools to realize his final goal: an objective system for the classification of hundreds of ragas. To accomplish this task, Ramamatya defined a highly effective distinction. He divided all ragas into two categories: a primary set called janaka ragas or mela ragas, and a secondary set, called janya ragas. Ramamatya describes the fundamental difference between these two classes of ragas in the following manner:
Sva. 4.1–2 — . . . I shall duly proceed to speak about the Melas, which cause their respective Ragas to be formed and which are distinguished by Raga-names, coined after the fashion of the languages prevailing in various provinces.[17] (Bold italics mine.)
This terse definition is significant for what it states, and for what it omits. (1) The key word here is cause. Ramamatya’s concept of cause and effect revolutionized Indian music because it permanently eliminated the earlier concept of origin. Ramamatya realized that no theorist could derive a plethora of ragas from only two gramas. (2) Conspicuously absent from his definition is the laksana–rasa or laksana–guna principle of his predecessors. Ramamatya probably decided against hierarchical classifications based on traditional technical properties and performance qualities because he knew that such considerations would complicate his system beyond comprehension. For an organizational arrangement to be effective, it must be simple, which in turn makes it memorable.
From his 12-tone tuning, Ramamatya selected various 7-tone scales. Since Sa and Pa are not subject to change, Ramamatya achieved diversity by selecting different combinations of five tones from the remaining ten tones. His objective was to identify, among the musical ragas of his time, one janaka (lit. parent) raga, or mela (lit. unifier) raga,[18] with seven tones that represent the largest number of janya (lit. born, or derived) ragas. The janya ragas have five, six, or seven tones in common with the mela ragas. When, in the latter case, two ragas consist of seven identical tones, Ramamatya named the mela raga after the best-known or exemplary raga. In this capacity, I refer to all such 7-tone ragas as denominative ragas. By definition, a denominative raga serves a double function: (1) it assumes a new technical identity as an abstract mela raga, and (2) it retains its original identity as a musical janya raga. Consequently, denominative ragas always occur twice in Ramamatya’s catalogs: the first time as mela ragas, and the second time as janya ragas. Furthermore, because Ramamatya considered all janya ragas equally important, the denominative ragas did not represent outstanding technical or musical characteristics. We conclude, therefore, that Ramamatya was the first theorist in the history of Indian music who used a mathematically determined tuning to define a system of raga classification based on the principle of musical abstraction. We may think of his mela ragas as tone pools that reflect the living musical raga traditions of his time!
Ramamatya’s mela ragas are now exclusively known as janya ragas. Some of these have vanished, others are known by different names, and a few have survived intact. For example, Figure 11.30(a) shows Ramamatya’s Mela Malavagaula, which has the same tones as Govinda’s modern Mela Mayamalavagaula. However, in Ramamatya’s treatise, Raga Malavagaula is described as a pentatonic raga;[19] this raga is now extinct. On the other hand, Venkatamakhi identifies the latter prototype as Mela Gaula,[20] and describes Raga Gaula as a hexatonic raga shown in Figure 11.30(a). Ramamatya also lists a janya raga of Mela Malavagaula called Raga Mechabauli,[21] which, like Raga Gaula, has survived into modern times as a janya raga of Mela Mayamalavagaula. In contrast, Figure 11.30(b) shows Ramamatya’s Mela Sri–raga and Raga Suddhabairavi,[22] both of which exist today as janya ragas of Govinda’s modern Mela Kharaharapriya. Ramamatya describes his two melas thus:
Sva. 4.11–12 — Ramamatya characterizes, with the approval of those that are well-versed in Raga (-Laksana), the Mela of ‘Malavagaula’ as consisting of these seven svaras, namely, Suddha Sa [C], Suddha Ri [Db], Suddha Ma [F], Suddha Pa [G], Suddha Dha [Ab], Cyutamadhyama Ga [E], and Cyutasadja Ni [B].
13–15 — Then do I enumerate some of the Ragas derived from this Mela (of Malavagaula); and they are: Malavagaula, . . . , Mechabauli, [etc.] . . .
16–17 — The Mela of ‘Sri–raga’ consists of these seven svaras, namely, Suddha Sa [C], Pañcasruti Ri [D], Sadharana Ga [Eb], Suddha Ma [F], Suddha Pa [G], Pañcasruti Dha [A], and Kaisiki Ni [Bb].
18–19 — Then do I enumerate some of the Ragas derived from this Mela (of Sri–raga); and they are: Sri–raga, . . . , Suddhabairavi, [etc.] . . . These and a few others also are derived from this Mela.[23] (Text in brackets mine.)
Figure 11.33 shows that Mela Malavagaula and Mela Sri-raga are identified in Venkatamakhi’s system as No. 15 and No. 22, respectively. In the previous quotation, note that the mela ragas always appear first in their respective list of janya ragas. Ramamatya applied this organizational principle throughout his catalogs of more than 60 janya ragas. Finally, as discussed in Section 11.32, do not confuse the mela ragas in Figure 11.30 with scales or musical ragas. Before Govinda’s time, most ragas did not consist of seven straight ascending tones and seven straight descending tones. Refer to Figure 11.30, which illustrates how Ramamatya would have intentionally performed a given janya raga on his vina by observing (1) varjya svara(s): omitting one or two notes in the ascent or descent, (2) vakra svaras: playing notes out of order in the ascent or descent, and/or (3) anya svara: using a foreign note not specified by the mela.[24] For example, with respect to the first two characteristics, Figure 11.30(b) shows that musicians play Sri-raga by omitting Ga and Dha in the ascent, and by playing two vakra passages — C1, Bb, G-A-Bb-G, F, D-Eb-D-C — in the descent. With regard to the third characteristic, Ramamatya’s Mela Hindola — called Mela Bhairavi by Venkatamakhi, and Mela Natabhairavi by Govinda (see Figure 11.33) — is now played as Raga Bhairavi with a foreign A natural in the ascent, and Ab in the descent.[25] In Ramamatya’s Svaramelakalanidhi, therefore, each mela raga functions as a tone pool from which musicians derive vast musical possibilities.

Sri-raga is the modern equivalent of the ancient Sadjagrama. In a highly insightful article, T.V. Subba Rao characterizes this raga by observing
. . . Sri-raga is the foremost and most auspicious . . . There is no doubt that the glory and sanctity attaching to this raga is to be attributed, apart from mythology, to its being the oldest of all scales, derived as it was as the first offspring of Sadjagrama. . .[26]
Although Ramamatya mentions the graha, amsa, and nyasa notes, he does not use traditional laksana properties to distinguish between groups of similar janya ragas that have five, six, or seven tones in common. Instead, he differentiates between such ragas according to pentatonic, hexatonic, or heptatonic forms. For example, Ramamatya classifies Raga Bhairavi and Raga Dhanyasi as janya ragas of Mela Sri-raga, but describes the former as a heptatonic raga, and the latter, as a pentatonic raga because it “. . . leaves [out] Ri and Dha.”[27] Later, in Venkatamakhi’s work, we encounter distinctions based on various varjya, vakra, and anya svara features. We conclude, therefore, that theorists gradually replaced the old laksana properties — i.e., the I, P, S, and F notes — with these new laksana properties. However, the Indian tradition of creating large groups of very similar sounding ragas, distinguished primarily by exquisite melodic subtleties, exists today as in the ancient past.
[1]Notable exceptions to the second generality are thousands of raga songs written by master composers Tyagaraja (1767–1847), Syama Sastri (1763–1827) and Muthuswami Diksitar (1775–1835), and others.
[2]Aiyar, M.S.R., Translator (1932). Svaramelakalanidhi, by Ramamatya, p. 43. The Annamalai University, India.
[3]Shringy, R.K., and Sharma, P.L., Translators (Vol. 1, Ch. 1, 1978; Vol. 2, Ch. 2–4, 1989). Sangitaratnakara, by Sarngadeva, Volume 1, pp. 141–146. Volume 1, Motilal Banarsidass, Delhi, India; Volume 2, Munshiram Manoharlal, New Delhi, India.
[4]Svaramelakalanidhi, p. 48.
[5]Ibid., p. 61.
[6]Ibid., pp. 48–49. Text in brackets from a slightly different translation on p. xxiii.
[7]Ibid., pp. 49–50.
[8]Ibid., p. 50.
[9]Sadie, S., Editor (1984). The New Grove Dictionary of Musical Instruments, Volume 3, p. 730. Macmillan Press Limited, London, England.
[10]Svaramelakalanidhi, pp. 52–53.
[11]Ibid., pp. 53–54.
[12]See Section 10.15.
[13]See Section 9.4.
[14]Svaramelakalanidhi, pp. 54–55.
[15]Since Ramamatya did not calculate the length ratios of his vina tuning, the possibility exists that even though he experienced the comma of Didymus, he was not aware of the comma of Pythagoras. A “disagreeable beat” between near-unisons or two tones that are close (as between two different E’s or two different B’s) is much easier to hear than between near-octaves or two tones that are distant (as between Db–C#1 or F#–Gb1). (For a description of the beat phenomenon, see Section 5.18.) This predicament illustrates a valuable lesson: sometimes the mind teaches the body to recognize distinctions not easily experienced through the senses. See Section 10.56, for a discussion of a similar problem encountered by Mersenne.
[16]See Section 10.15.
[17]Svaramelakalanidhi, p. 55.
[18]Kaufmann, W. (1976). The Ragas of South India, p. xvi. Indiana University Press, Bloomington, Indiana.
Raga names and technical terms differ significantly among various Indian texts. In most cases, I have chosen to use Kaufmann’s spellings throughout the sections on South Indian and North Indian music.
[19]On p. 63 of the Svaramelakalanidhi, Ramamatya states,
“Sva. 5.40 — That [Janya] Raga is called Malavagaula, which is Audava [Pentatonic], for it leaves Ri and Pa, though, at times they are retained. (Text in brackets mine.)”
In pentatonic or hexatonic forms, Raga Malavagaula or Raga Gaula, respectively, do not include all seven tones of the mela. With respect to Mela Malavagaula, T. V. Subba Rao observes in his essay, “The ragas of the Sangita Saramrita,” p. 127, that theorists have questioned “. . . the wisdom of calling a mela by the name of a raga which is not sampurna [lit. complete; i.e., heptatonic].” See Note 26.
[20]The Ragas of South India, p. 123.
[21]Ibid., p. 143.
[22]Ibid., p. 263, 311.
[23]Svaramelakalanidhi, p. 56.
[24]Sambamoorthy, P. (Vol. 1, A–F, 1952; Vol. 2, G–K, 1959; Vol. 3, L–N, 1971). A Dictionary of South Indian Music and Musicians. The Indian Music Publishing House, Madras, India.
I have used this useful but unfortunately incomplete dictionary throughout the chapter on Indian Music. Definitions for varjya ragas, vakra ragas, and anya ragas (bhasanga ragas) occur in Volume 2, p. 253.
[25](a) Powers, H.S. (1958). The Background of the South Indian Raga-System, pp. 20–21. Ph.D. dissertation printed and distributed by University Microfilms, Inc., Ann Arbor, Michigan.
This dissertation is a valuable source for the study of South Indian music and terminology. The last part includes transcriptions of LP recordings of compositions by Tyagaraja, Sastri, Diksitar, and others.
(b) The Ragas of South India, pp. 206–207.
[26]Rao, T.V.S. (1945 and 1946). The ragas of the Sangita Saramrita, pp. 63–64. The Journal of the Music Academy XVI, Parts I–IV, pp. 45–64, and XVII, Parts I–IV, pp. 104–134, Madras, India.
[27]Svaramelakalanidhi, pp. 62–63.