ON THE ART AND SCIENCE OF ACOUSTIC INSTRUMENTS
© 2000–2025 Cris Forster
CHAPTER 11: WORLD TUNINGS
Part IV: Arabian, Persian, and Turkish Music
Section 11.53
The most famous and complex Arabian treatise on music is a work entitled Kitab al-musiqi al-kabir (Major Book on Music),[1] by Al-Farabi (d. c. 950). Although the author does not describe the construction of a canon in his Instrumentarium,[2] he makes this pivotal observation:
We will start by giving a concise . . . description of the lute, because, of all the stringed instruments, it is the most popular. It belongs to the family of instruments that are equipped with strings on which one plays different sections to produce different notes.
On the neck of this instrument, frets pass under the strings and delimit on each one of them the different sections that produce the notes. These frets play the role of bridges; one places them parallel to the lower part of the instrument known as the [bridge].[3] (Bold italics mine. Bold italics in brackets my correction of the “cordier” translation error in La Musique Arabe.)
I interpret the statement, “These frets play the role of bridges,” as a reference to canon bridges. As discussed above, canon bridges may be moved and repositioned anywhere along a string’s length. By now, this observation seems redundant, but a careful reading of the Kitab al-musiqi al-kabir reveals that Al-Farabi defined many scales and modes that are not playable given the notes of his 10-fret and 12-fret ‘ud tunings. For example, a tetrachord discussed in Section 11.56 requires ancient length ratio 81/70. Because this ratio does not exist on the latter ‘ud, Al-Farabi accurately describes the exact location that, when provided with a moveable fret, produces the desired tone. So, we must be extremely cautious not to begin this discussion on Al-Farabi by assuming that his fret descriptions represent inflexible tuning systems. Unlike a modern guitar that has rigid metal frets embedded in the fingerboard, an authentic lute built in either the Middle East[4] or in Europe[5] has moveable frets that consist of gut strings tied around the instrument’s neck. Consequently, a lute player tunes and retunes a lute by moving its frets in the same manner as a canon player tunes and retunes a canon by moving its bridges.
Al-Farabi describes the 10-fret ‘ud tuning in the following manner:
The most commonly used frets are four in number; they are placed on the neck [of the lute] so that the fingers may reach them as easily as possible . . . The first [fret] is that of the index finger, the second, of the middle finger, the third, of the ring finger, and the fourth, of the little finger. The sections we generally use on each string of the lute are, of course, equal in number to the commonly used frets. The first note generated by each string is rendered by the whole string; it is known as the open string. The second [note] is called that of the index finger; the fret that delimits the string section which generates it is placed at 1/9 of the distance between the meeting point of the strings [the nut] and the bridge.
[ Fret 5: → 9/8 = 204 ¢ ]
The third note is that of the middle finger; we will not discuss here the fret that delimits the string section which produces it. We will return to it when we deal with that note. The fourth is that of the ring finger; the fret that delimits the section which produces it is placed at 1/9 of the distance between the index finger fret and the bridge.
[ Fret 9: → 81/64 = 408 ¢ ]
The fifth note is that of the little finger; its fret is placed at 1/4 of the distance between the meeting point of the strings and their other ends attached to the bridge.
[ Fret 10: → 4/3 = 498 ¢ ]
We see that the notes produced by one of the strings of the lute played open, then with the little finger fret, are at an interval of a fourth; those generated by the open string and the index finger fret are at an interval of a tone; and those rendered by the open string and the ring finger fret, at a ditone. The notes produced by a string stopped at the ring finger fret, then at the little finger [fret], are thus separated by the interval called a remainder [limma].
[ Interval ratio: 4/3 ÷ 81/64 = 256/243 = 90 ¢ ]
The most commonly used frets of the lute therefore delimit the intervals of the strong diatonic genus.
The strings of the lute are stretched, according to common practice, so that the second [Mathlath] produces, when it is played open, a note identical to that given by the first [Bamm] stopped at the little finger fret; the third open string [Mathna] must produce a note identical to that of the little finger fret of the second [Mathlath]; and the open fourth [Zir] gives a note like that of the little finger fret of the third [Mathna].
Each open string therefore produces a note that is at an interval of a fourth from . . . the string placed below it. . . .
Let us call the meeting point of the strings A. . . .
Let us also label the points of contact of the strings with the frets: the points of contact of the index finger fret will be respectively Z, Ḥ, Ṭ, Y; those of the ring finger fret: K, L, M, N; and those of the little finger fret: S, Ἁ, F, Ḍ. . . .
We sometimes place the middle finger fret above that of the little finger, towards the nut, at a distance corresponding to 1/8 of that which separates the latter fret [the little finger] from the bridge.
[ Fret 6: → 32/27 = 294 ¢ ]
The note of the middle finger fret and that of the little finger fret are then in the ratio of 1 + 1/8 [9:8].
[ Interval ratio: 4/3 ÷ 32/27 = 9/8 = 204 ¢ ]
We use this middle finger when the intervals of the strong diatonic genus are arranged [descending] from the upper [note] . . . [as in descending from 4/3, or 4/3 ÷ 9/8 = 32/27]; in that case, the note delimiting the second interval of the diatonic genus inverted [as in descending from 32/27, or 32/27 ÷ 9/8 = 256/243] falls between the open string [1/1] and that of the index finger fret [9/8]; we sometimes use this note [256/243], but more often it is omitted.
Other musicians place the middle finger fret halfway between that of the index finger and that of the [ring finger]; it is then called the Persian middle finger.
[ Fret 7: → 81/68, = 303 ¢ ]
Finally, others place it halfway between the Persian middle finger we have just discussed and the ring finger fret; it is then the fret of the middle finger of Zalzal.
[ Fret 8: → 27/22 = 355 ¢ ]
The middle finger fret that results from the inversion of the intervals of the strong diatonic genus is not considered by musicians to be a middle finger fret; when they use it, they call it the neighbor of the middle finger, but they recognize as a true middle finger only the fret of the Persian middle finger, or that of the middle finger of Zalzal.
We again represent the four strings of the lute, but this time we show the fret of the [Persian] middle finger; the points of contact of this fret with the strings will be respectively: Q, R, Š, T.
In the playing of the lute, we also use frets placed between that of the index finger and the nut; they are called the neighbors {sing. mujannab, pl. mujannabat} [or, anterior frets] of the index finger. [Al-Farabi does not give instructions for calculating the location of the first anterior, which I call Fret 1, and which is the first fret in Al-Farabi’s table below; in the context of ratios, he only mentions the following interval ratio between Fret 1 and Fret 10.] One of these is at an interval of a ditone [or, 9/8 × 9/8 = 81/64] from the little finger;
[ Fret 1: 4/3 ÷ 81/64 = 256/243 = 90 ¢ ]
another is placed halfway between the nut and the index finger fret;
[ Fret 2: → 18/17 = 99 ¢ ]
another [is] halfway between the nut and the fret of the Persian middle finger,
[ Fret 3: → 162/149 = 145 ¢ ]
or [halfway between the nut and the fret] of the middle finger of Zalzal.
[ Fret 4: → 54/49 = 168 ¢ ]
If we count the notes provided by all the frets we have just discussed, plus those given by the strings in their open length, we find that each string produces [eleven] notes. In the table below, we give the numeric value of each of these notes, using the smallest integers that allow us to express their ratios exactly.

We will again represent the four strings of the lute, and mark on them the two frets of the middle finger, the neighbor of the middle finger, and the neighbor of the index finger resulting from the inversion of the diatonic genus. The points of contact of the fret of the middle finger of Zalzal with the four strings are labeled: Th, H, Dh, Ṣ; those of the neighbor of the index finger: B, J, D, H; and those of the neighbor of the middle finger: Ḍh, Ġ, W, LA.[6] (Text, numbers, and ratios in brackets mine. Bold italics in brackets my corrections of unedited errors in La Musique Arabe. Mujannab in braces in Farmer’s The Music of Islam.)
Figure 11.47 illustrates these ten divisions in the order described by Al-Farabi, Table 11.23 gives detailed ratio calculations, and Figure 11.48 is a fret diagram of the tuning. In the quote below, Al-Farabi explains that these frets do not belong to an actual instrument, but rather, that they represent the maximum number of tones utilized by practicing musicians. Furthermore, Al-Farabi probably neglected to include the note names of Frets 2, 3, and 4 because “certain musicians” did not use them:
The frets we have enumerated are nearly all those that one ordinarily uses on the lute. However, one does not find them all together on the same instrument. There are some that are essential to the playing of the lute and used by all musicians. These are the index finger fret [9/8], that of the ring finger [81/64], that of the little finger [4/3], and one among those that are placed between the index finger and the ring finger frets and which everyone calls middle finger frets; for some this will be the middle finger of Zalzal [27/22], for others the Persian middle finger [81/68], for still others the fret that we have called the neighbor of the middle finger [32/27].
As for the frets called the neighbors of the index finger, certain musicians reject them and do not use any of them. Others use one of the middle finger frets and employ with it the neighbor of the middle finger, which they consider to be a unique entity and not as a middle finger fret, but they don’t use any of those called neighbors of the index finger; still others use all together one of the two middle finger frets, the neighbor of the middle finger, and one of the frets known as neighbors of the index finger, namely, the one that is separated by an interval of a limma from the index finger fret.[7] (Ratios in brackets mine.)
Al-Farabi does not include the last fret — 9/8 ÷ 256/243 = 2187/2048 = 114 ¢ — which produces the Greek apotome. However, it does appear in Al-Farabi’s 12-fret tuning. (See Section 11.54.) In his commentary on the 10-fret tuning, Al-Farabi also describes a second extra fret that functions as an alternate middle finger of Zalzal.
The fret of the middle finger of Zalzal is sometimes placed above that of the ring finger, towards the index finger, at a distance corresponding to an interval of a limma.[8]
This unusual fret — 81/64 ÷ 256/243 = 19683/16384 = 318 ¢ — represents D#, or the ninth “fifth” in the ascending spiral of “fifths” in Chapter 10, Figure 16(a). Although this tone may be found on the traditional tunbur of Khurasan (see Figure 11.70), it does not appear in any other ‘ud tuning.
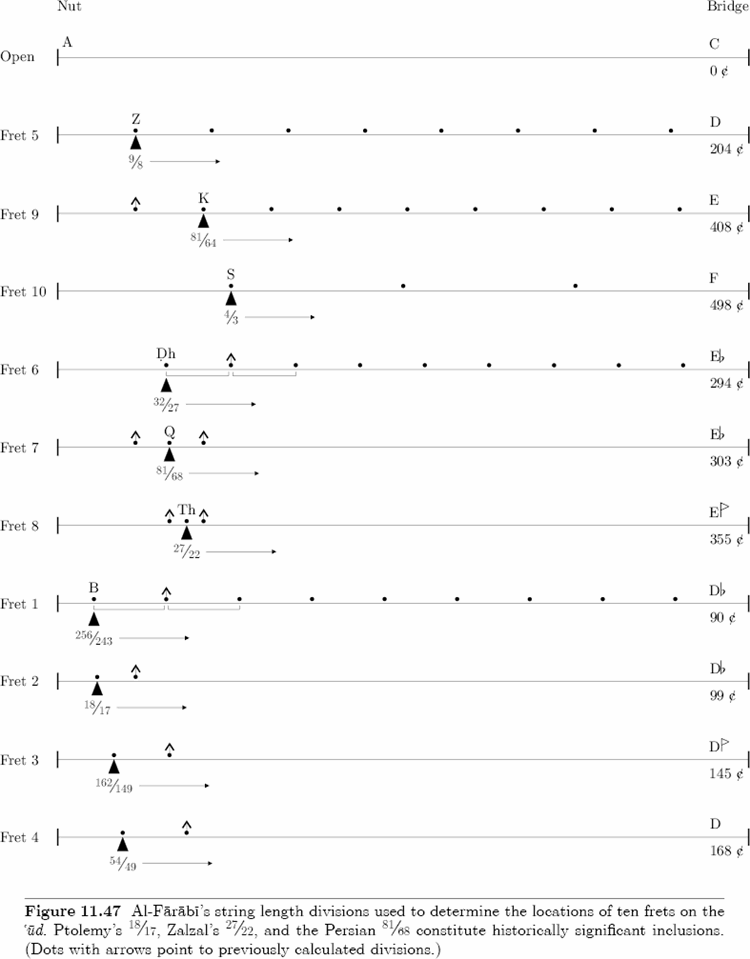

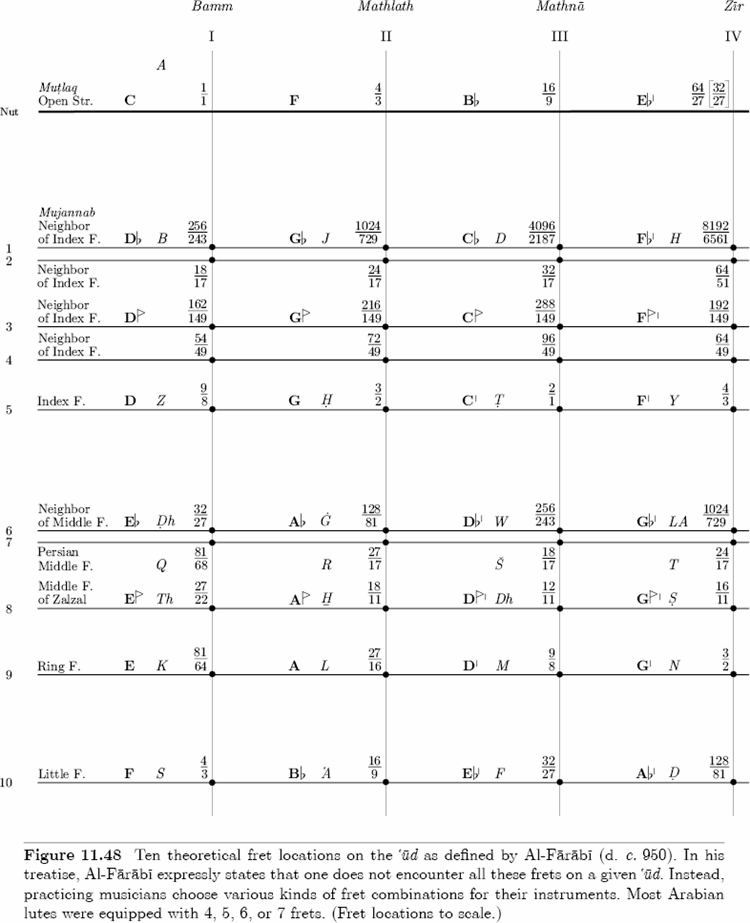
Figures 11.47 and 11.48 include several historically significant ratios. As discussed in Chapter 10, Section 31, length ratio 18/17, which results from an arithmetic division of length ratio 9/8, was first defined by Claudius Ptolemy (c. A.D. 100 – c. 165) in his great work Harmonics. Al-Farabi’s descriptions of “semitone” 18/17, and of just “quarter- tones”: 36/35, 35/34, 34/33, and 33/32 appear in Chapter 10, Section 31, as well.
Al-Farabi is the first theorist to record two second finger frets called the Persian middle finger and the middle finger of Zalzal. The former, ratio 81/68 [303 ¢] is slightly higher than the Pythagorean “minor third,” ratio 32/27 [294 ¢], of the Old Arabian School. A factorization shows that composite number 68 is a product of primes 2 × 2 × 17.[9] As a result, the denominators of the Persian middle finger fret, ratio 81/68, and of the Ptolemaic index finger fret, ratio 18/17, have prime number 17 in common. Consequently, the interval of a “whole tone” exists between these two frets: 81/68 ÷ 18/17 = 9/8.
The middle finger of Zalzal was named after the famous lutenist Mansur Zalzal (d. 791).[10] He is credited with the implementation of length ratio 27/22 [355 ¢], known in the West as the “neutral third” because it approximates the average between the Pythagorean “major third,” ratio 81/64 [408 ¢], and the Pythagorean “minor third”; or (408 ¢ + 294 ¢) ÷ 2 = 351 ¢. Throughout the following discussions on Al-Farabi and Ibn Sina, we will use the modern Persian koron sign: k, which indicates a tone that is approximately 30–70 ¢ flat of a given standard Pythagorean pitch, and the modern Persian sori sign: s, which indicates a tone that is approximately 30–70 ¢ sharp of given standard Pythagorean pitch. In his book and dissertation entitled The Dastgah Concept in Persian Music, Hormoz Farhat[11] distinguishes between such tones and the notorious tempered “quarter-tone” — 50.00 ¢ exactly — of Western music:
In our notation, the neutral step above c is shown as dk, and the neutral step above d is shown as ek, after the accepted system of notation in Persia today. Even though the signs k and s were invented by A.N. Vaziri [1886–1981], and were to suggest a quarter-tone flat, and a quarter-tone sharp, respectively, and although we have discussed and rejected the quarter-tone system, we see no reason why these signs which are now part of the Persian alphabet of notation, cannot be used to good advantage.[12] (Dates in brackets mine.)
Koron stands for the half flattening of a pitch, or, shall we say, for the lowering of a pitch by a microtone. … [Sori] stands for half sharp, or [the] raising of a pitch by a microtone.[13] (Text in brackets mine.)
Note, therefore, that in the context of Al-Farabi’s 10-fret tuning, the descending chromatic sequence that includes Fret 8 appears as 81/64 [E], 27/22 [Ek], 32/27 [Eb]; similarly, the descending chromatic sequence that includes Fret 3 appears as 9/8 [D], 162/149 [Dk], 18/17 [Db].
Al-Farabi also identified the just “quarter-tone,” interval ratio 33/32, in his commentary on the 10-fret tuning. He gives this description in the context of the alternate middle finger of Zalzal, ratio 19683/16384 [D#], discussed above. Al-Farabi criticizes the use of the latter fret because the interval between the ring finger, ratio 81/64, and the middle finger of Zalzal should not be a limma: 81/64 ÷ 19683/16384 = 256/243 = 90¢. Instead, the interval between the ring finger and the middle finger of Zalzal should be a just “quarter-tone,” which can only be produced by the standard middle finger of Zalzal: 81/64 ÷ 27/22 = 33/32 = 53 ¢.
But we say that this procedure [which produces ratio 19683/16384] is bad, because the fret of the middle finger of Zalzal, placed in this manner, is necessarily at an interval of a limma [256/243] with that of the ring finger, and not at a quarter-tone [33/32] as it should be according to what was said above . . .[14] (Bold italics, and text and ratios in brackets mine.)
Section 11.54
Before we continue with Al-Farabi’s 12-fret ‘ud tuning — which results in a 22-tone “double-octave” scale — let us first consider his intellectual reasons and musical motivations for creating this scale:
Let us now proceed to the instruments which give us the natural notes, and to the one of them which gives us the greatest quantity and the most perfect of notes — namely, the ‘ud.
Evidently, if we assume pitches separated by definite intervals, we may equally assume within those intervals, other pitches. However, since our purpose is to select therefrom the pitches of a single jins {Arabicized from the Greek “genus”; Arabic pl. ajnas} (from which alone natural tunes are composed) we would not need to consider those, {or} all the pitches which can emerge between these intervals. The first intervals are natural; the [other] intervals in between them which might be used are considered unnatural, even though they are similar.
It may happen that some of the intervals between the notes of a jama‘ah [“collection” or scale] are natural while others are unnatural. For the most part, the well known intervals used on the instruments are those which should be regarded as essentially natural. On the other hand, it is also necessary to count as somewhat natural those intervals which are sometimes or rarely regarded as natural. This results from the fact that much of that which is unnatural in itself would become natural if it were combined with something else. Let us then consider all [the intervals] that are used in the tunes reproducible by the ‘ud, even if they are only used rarely.[15] (Bold italics, and text in braces mine. Text in parentheses and brackets in Al-Faruqi’s dissertation.)
Al-Farabi’s perspective on the presence of “other pitches,” on the possibility of “intervals between notes,” and on the process by which the “unnatural becomes natural” expresses the conviction of a powerful intellect and the expanse of a limitless imagination. He then continues with this ‘ud tuning description:
Let us tune the lute in the usual manner, and assign the lowest tone to the open string Bamm. Its octave equivalent is the note produced by the index finger on the Mathna string. Evidently, this instrument is not meant for a single octave, but also [includes] those notes which are beyond the limits of the first octave collection.
If, thereafter, we seek the upper octave equivalent of the index finger on the Mathna string, we would not find it in the finger positions of the ‘ud. In order to complete the second of the octaves of pitches, let us stretch a fifth string. We would then find completion of the second octave in the ring finger tone of the Hadd or fifth string.
It is evident that the notes in the second octave ought to be notes [equivalent to] the first octave and vice versa. Whenever the notes of a melody are found in one of the octaves produced by certain instruments, and not in the other octave, we would conclude that the latter octave has some notes missing and that one octave had been made shorter than the other. The two octaves should be made equal in the number of notes [they contain] so that every note from one octave matches one from the other octave . . .
If we compare the notes of the first octave and those of the second, we find that the tone produced by the index finger on the Mathna {2/1} has the same pitch as that of the open string Bamm {1/1}. And if we move from the open string Bamm to its index finger position {9/8}, we find an equivalent [for the latter] produced in the second octave by the ring finger on the Mathna. We may then conclude that the interval between the tones produced by the open string Bamm and its index finger fret is equal to that between the index finger fret on the Mathna and its ring finger fret.
Of the three middle finger positions used, let it suffice for us to consider one of them, the wusta al Zalzal. If we descend to the Zalzal middle finger position on the Bamm {27/22}, we would find no note equivalent to it in the second octave. The same is true of the ring finger position on the Bamm {81/64}. If we were to establish equivalencies for them in the second octave, the pitch of the ring finger on the Bamm would be found above the index finger position, close to the ‘anf on the Zir string. The note equivalent to that produced by the middle finger on the Bamm is above that found near the ‘anf of the ‘ud on the Zir string.
The note equivalent to that of the little finger on the Bamm {4/3} and the open string Mathlath {4/3} is the index finger note on the Zir. That comparable to the index finger note on the Mathlath {3/2} is found by the ring finger on the Zir. Finally, for the middle and ring finger notes on the Mathlath {18/11 and 27/16}, we do not find any positions in the second octave. If we sought to reproduce them, we would find an equivalent to the note produced by the ring finger on the Mathlath {27/16} above the index finger on the fifth string. The {equivalent of the note} of the . . . middle finger {position} on the Mathlath {18/11} {is} still farther up on the fifth string. The note of the open string Mathna {16/9} is equivalent to the index finger note on the fifth string. The note produced by the index finger on the Mathna {2/1} is equivalent to that produced by the ring finger on the fifth {4/1}. The second octave therefore includes all the notes of the first octave.[16] (Bold italics, and text and ratios in braces mine. Text in parentheses and brackets in Al-Faruqi’s dissertation.)
Although Al-Farabi begins by stating, “Let us tune the lute in the usual manner . . .” not until this last sentence are we able to deduce his original set of frets that produce the lower “octave.” In Figure 11.49, circles indicate that his original tuning consists of a 9-tone scale: 1/1 [C], 9/8 [D], 27/22 [Ek], 81/64 [E], 4/3 [F], 3/2 [G], 18/11 [Ak], 27/16 [A], 16/9 [Bb], 2/1 [C1].[17] The latter nine tones are located on the following four frets: 9/8, 3/2, and 2/1 on Fret 6; 27/22 and 18/11 on Fret 9; 81/64 and 27/16 on Fret 11; and 4/3 and 16/9 on Fret 12. Consequently, to realize upper “octave” equivalents for 27/22 and 81/64 on the Bamm, and for 18/11 and 27/16 on the Mathlath, Al-Farabi installs Frets 1 and 4 across the Zir and Hadd. All the tones marked with circles in the lower “octave” now have equivalents marked with circles in the upper “octave.”
With respect to the tones contained in the upper “octave” but missing in the lower “octave,” in Figure 11.49 diamonds indicate five such scale degrees. Al-Farabi continues his description by observing that ratios 12/11, 16/11, and 64/33 on Fret 9 have no equivalents, and ratios 32/27 and 128/81 on Fret 12 also have no equivalents. To remedy these deficiencies he installs Fret 5 to match the three former tones of Fret 9, and Fret 7 to match the two latter tones of Fret 12. He then decides that ratios 256/243, 1024/729, and 4096/2187 on Fret 7 should also have equivalents, and therefore installs Fret 2. Next, he decides that ratios 8192/6561 and 32768/19683 on Fret 2 of the Zir and Hadd, respectively, should have equivalents, and so he installs Fret 10. Then, Al-Farabi states that if one includes the Persian middle finger fret, which produces ratios 18/17, 24/17, and 32/17 on the Mathna, Zir, and Hadd, respectively, one must also install Fret 3 to realize equivalents for these three degrees in the lower “octave.”[18] Al-Farabi concludes
After these, no note of the ‘ud remains which needs to be reproduced. In each octave, there are twenty-two notes; and these are all the notes used by the ‘ud. Some of them are more frequently used than others.[19]
An examination of Al-Farabi’s 22-tone “double-octave” scale reveals that it contains all the degrees of Al-Kindi’s 12-tone “double-octave” scale. Al-Farabi’s comments regarding the tuning of two identical “octaves” is a lesson he undoubtedly learned from Al-Kindi. Throughout his writing, Al-Farabi demonstrates a capacity to assimilate the knowledge of masters who lived before him. As discussed below, he fully incorporated the works of Aristoxenus and Ptolemy into his theory of tetrachords. Moreover, he always interlaced such discussions with his own ideas and interpretations. Like Marin Mersenne in the West, Al-Farabi consistently contemplated the possibility of expanding his experiences through instruments and tunings designed to transcend ordinary musical standards.[20] This explains why we will encounter minor contradictions in his description of customary practices. (See Section 11.55 and Figure 11.53.)

Section 11.55
Reminiscent of Al-Munajjim’s statements that describe permissible tone combinations of eight ancient modes, Al-Farabi continues the discussion by defining compatible and incompatible notes, and ends his analysis with three standard modes.
Groupings of compatible notes and scales
Among these frequently used notes, those of the ring finger and the middle finger on the same string cannot be used together in the same melody as basic notes. The same applies to their upper and lower octave equivalents. On the other hand, the notes produced by the strings played open and those produced by the little finger fret on each {string}, as well as their octaves, are combined with all the notes in the composition of modes. The index finger note on a string will agree with that of the middle finger or the ring finger; likewise, the octave equivalents of these notes. The ring finger and the middle finger notes of the same string are therefore not compatible.
In the same cycle (scale), the notes of the strings played open {C, F, Bb}, those of the little finger {F, Bb} and the index finger {D, G}, will agree either with those of the middle finger {Ek, Ak} or with those of the ring finger {E, A}; they {the notes C, D, F or F, G, Bb} are (compatible) in the same genus with the notes of one or the other of those two frets. When one (scale) contains the ring finger notes and the degrees that are of the same genus {C, D, E, F or F, G, A, Bb}, to associate other notes to it would not always be to add to its perfection; the same is true when the mode is formed of the middle finger notes and the degrees that are of the same genus {C, D, Ek, F or F, G, Ak, Bb}.
Taking into account only the notes produced by the ring finger fret {E, A} and their compatible degrees {C, D, F, G, Bb}, or only the middle finger notes {Ek, Ak} and their compatible degrees {C, D, F, G, Bb}, the two cycles (the two octave scales) altogether will include fourteen notes, i.e., seven degrees for each {scale}.
The Persian middle finger notes {Eb, Ab} are not compatible either with the ring finger notes {E, A} or with those of the middle finger of Zalzal {Ek, Ak}, but they are of the same genus as those of the index finger, the little finger, and the strings played open. Taking into account only the Persian middle finger notes {Eb, Ab} and their compatible degrees {C, D, F, G, Bb}, each cycle (each octave scale) will include seven degrees of the same genus.
These are the various kinds of compatible notes used by the aforementioned peoples to compose their melodies. As a result, there are three categories of compatible notes that we can organize in each of the two cycles of the scale [of the double octave].
The first kind of notes of the same genus will include the following notes: that which is produced by the first open string of the lute, the index finger note of this same string, that of its ring finger, and that of its little finger, which is identical to that of the second open string; then the index finger of the second string, its ring finger and its little finger {C, D, E, F, G, A, Bb}.
The second will include the following degrees: the note of the first open string, that of its index finger, its middle finger of Zalzal, and its little finger; then the index finger of the second string, its middle finger of Zalzal, and its little finger {C, D, Ek, F, G, Ak, Bb}.
Finally, the third kind of compatible notes will include: the note of the first string played open, that of the index finger of this same string, that of its Persian middle finger, that of its little finger; then those of the index finger of the second string, its Persian middle finger, and its little finger {C, D, Eb, F, G, Ab, Bb}.
These are the three categories of natural and compatible notes used in the composition of melodies. We could admit others, but they would give birth to a weakly consonant and non-harmonious music.[21] (Bold italics, and text in braces mine. Text in parentheses and brackets in La Musique Arabe.)
Figure 11.50 shows that all three modes consist of seven tones, or two identical conjunct tetrachords that span the intervals from 1/1 to 4/3, and from 4/3 to 16/9. In response to Al-Farabi’s repeated use of “equivalents,” this figure also includes the “octave” of each mode. Finally, I named these genera the ‘Diatonic Mode’, the ‘Mode of Zalzal’, and the ‘Persian Mode’ to emphasize the musical quality that gives each mode a unique identity. In the context of scales, the ‘Diatonic Mode’ is distinguished by a “major third” and “major sixth,” the ‘Mode of Zalzal’ by a “neutral third” and “neutral sixth,” and the ‘Persian Mode’, by a “minor third” and “minor sixth.” The latter two tones, 81/68 [303 ¢] and 27/17 [801 ¢], are aurally indistinguishable from the “minor third” [300 ¢] and the “minor sixth” [800 ¢] of 12-tone equal temperament.
Given a tuning where the tonic sounds C, Al-Munajjim and Al-Farabi both agree that the note of the ring finger — 81/64 [E] — and the notes of the middle finger — either 27/22 [Ek] or 81/68 [Eb] — are incompatible in the same melody. We are here again reminded of the profound consequences of these “. . . three categories of compatible notes . . .” The ‘Diatonic Mode’ and the ‘Persian Mode’ are essentially identical with the major tonality and the minor tonality, respectively, of Western music. In contrast, for most occidental musicians the ‘Mode of Zalzal’ remains unknown.

Al-Farabi concludes this discussion on the three standard modes with the following observations:
We therefore say that a cycle will always include seven degrees of the same genus. This is derived from the statements of certain skillful musicians {like Al-Kindi}, who have long practiced this art and who have investigated the natural notes, contrary to what may be taught by certain masters incapable of furnishing tangible evidence for what they assert in their books, not having educated their ear by listening to music. What the latter say may be partly true; but the notes they include between the two ends of the scale are not all compatible. Their statements enable us, however, to prove that these degrees can be but seven in number, neither more nor less, {although the number of degrees} of the {octave} in general is infinite.
The majority of theorists known to us do not seek to establish the compatible notes within octaves. Some are solely concerned with the notes capable of having an octave equivalent; others want to establish the number of all the musical notes, whether or not they have an octave equivalent. These theorists therefore cannot agree upon the number of musical degrees. Among those who wanted to establish in books the number of all the notes reproducible at the octave, we have to count the Greek mathematicians of antiquity and the Arab empire theorists of our time. Among the latter, some followed the way of the Greek mathematicians, others disregarded it; as skillful practitioners, trained in music, they trusted only their ears. Their vast experience dictated to them what to assert in their writings. Their musical instinct, driving them to the realization of the aforementioned three musical forms, led them to assign a number to the degrees of the scale. They are thus closer to the truth than those theorists of our time who wanted to follow the way of the ancient Greek mathematicians. They followed them, but they did not possess their knowledge or the experience and esthetic sense of more recent practitioners. Confident in the science of the ancients, they merely repeated their words; but one sees that they are incapable of explaining or proving what they assert. In a work where we report the opinions of all authors who have dealt with music, we mention those writers of whom we have just spoken, by pointing out the questions they could solve and those they were unable to solve.
It is evident that, for instruments with open strings, the number of notes in octaves will still be that which we have established. If a string of one of these instruments is tuned to the ring finger [of one of the strings] of the lute, one cannot tune another to the middle finger [of this same string], and if one tunes to the middle fingers, one cannot tune at the same time to the ring fingers. The scale of sounds produced by instruments with open strings will thus contain no more than seven degrees.[22] (Text in braces mine. Bold italics in braces my correction of the “dynamis” translation error in La Musique Arabe. Text in brackets in La Musique Arabe.)
[1]Farmer, H.G. (1965). The Sources of Arabian Music, p. 28. E.J. Brill, Leiden, Netherlands.
This work consists of an annotated bibliography of 353 Arabian texts on music from the 8th through the 16th century. Throughout my text, book titles in parentheses refer to Farmer’s English translations of Arabian titles.
[2]Ibid., p. xx.
Farmer observes, “The first description of instruments of music in any language was contributed by Al-Farabi, and that was six hundred years before any other land had considered the subject sufficiently interesting for serious study.”
[3](a) D’Erlanger, R., Bakkouch, ‘A.‘A., and Al-Sanusi, M., Translators (Vol. 1, 1930; Vol. 2, 1935; Vol. 3, 1938; Vol. 4, 1939; Vol. 5, 1949; Vol. 6, 1959). La Musique Arabe. Volume 1, p. 166. Librairie Orientaliste Paul Geuthner, Paris, France.
(b) Farmer, H.G. (1978). Studies in Oriental Musical Instruments, First and Second Series. Second Series, p. 65. Longwood Press Ltd., Tortola, British Virgin Islands.
The Arabic term for a bridge-string holder is musht. This simple part consists of a long, narrow, and flat piece of wood that has numerous notches and holes through which one threads and fastens the strings. As such, a musht functions exactly like the bridge-string holder of a modern acoustic guitar. It is glued directly to the top plate near the round end of the ‘ud, and therefore transmits mechanical energy from the vibrating strings to the soundboard. On an ‘ud, the measured length of an open string is defined by the distance between the nut — or ‘anf (lit. nose) — and the bridge — or musht (lit. comb).
Before we continue with this discussion on scales and modes, we must first address several problems with respect to modern French and English translations of ancient Arabic texts. The treatises of the six theorists mentioned at the beginning of Section 11.45 comprise the first four volumes of a six-volume work entitled La Musique Arabe, published posthumously by Baron Rodolphe D’Erlanger (1872–1932). Regrettably, with regard to mechanical instrument components, the translations of critical words in these volumes are often incorrect. For example, the translators consistently translate the Arabic word musht with the French word “cordier.” The modern term “cordier” refers to the “tailpiece” found on all instruments of the violin family. On a violin, a cordier consists of a tapered piece of curved wood to which one fastens the strings at the ends opposite to the tuning pegs. The cordier is situated between the bridge and the lower end of the violin, and the tension of the strings suspends the cordier above the violin’s top plate, or soundboard. Consequently, the cordier does not contact the top plate, which means that it does not transmit mechanical energy from the vibrating strings to the soundboard. Furthermore, with the exception of a few plucked instruments like mandolins and banjos, the vast majority of instruments that have Western-style tailpieces are bowed instruments. Finally, note that on an instrument equipped with a cordier, all strings have two different lengths: a measured length between nut and bridge, which defines the critical vibrating length of the open strings, and an extended length between nut and tailpiece, which is completely irrelevant to the tuning and playing of the instrument.
[4]Studies in Oriental Musical Instruments, Second Series, pp. 64–65.
[5]Crookes, D.Z., Translator (1986). Syntagma musicum II: De organographia, Parts I and II, by Michael Praetorius, p. 69. The Clarendon Press, Oxford, England. The first edition of this work was published in 1618.
[6](a) Forster Translation: in La Musique Arabe, Volume 1, pp. 166–174.
(b) Farmer, H.G. (1957). “The Music of Islam.” In New Oxford History of Music, Volume 1: Ancient and Oriental Music, E. Wellesz, Editor, p. 460. Oxford University Press, London, England, 1960.
[7]Forster Translation: in La Musique Arabe, Volume 1, p. 179.
[8]Forster Translation: in La Musique Arabe, Volume 1, p. 174.
[9]See Chapter 10, Section 1.
[10]Studies in Oriental Musical Instruments, Second Series, p. 49.
[11](a) Farhat, H. (1965). The Dastgah Concept in Persian Music. Ph.D. dissertation printed and distributed by University Microfilms, Inc., Ann Arbor, Michigan.
(b) Farhat, H. (1990). The Dastgah Concept in Persian Music. Cambridge University Press, Cambridge, England.
[12]The Dastgah Concept in Persian Music (1965), p. 26.
[13]Ibid., p. 44.
[14]Forster Translation: in La Musique Arabe, Volume 1, p. 174.
[15](a) Al-Faruqi, L.I. (1974). The Nature of the Musical Art of Islamic Culture: A Theoretical and Empirical Study of Arabian Music, pp. 406–407. Ph.D. dissertation printed and distributed by University Microfilms, Inc., Ann Arbor, Michigan.
In Appendix III, pp. 404–455 consist of translated excerpts from Al-Farabi’s Kitab al-musiqi al-kabir.
(b) La Musique Arabe, Volume 1, pp. 44–45.
[16](a) The Nature of the Musical Art of Islamic Culture, pp. 407–411.
(b) La Musique Arabe, Volume 1, pp. 45–48.
[17]Note that Al-Farabi’s original 9-tone scale is similar to the 10-tone scale of the Old Arabian School in Figure 11.42(b).
[18](a) The Nature of the Musical Art of Islamic Culture, pp. 411–412.
(b) La Musique Arabe, Volume 1, pp. 48–49.
[19](a) The Nature of the Musical Art of Islamic Culture, p. 412.
(b) La Musique Arabe, Volume 1, p. 49.
[20]Comparisons to Marin Mersenne (1588–1648) are truly striking. For example, Chapter 10, Table 29, shows Mersenne’s expansion of the trumpet marine tuning, which in principle resembles Al-Farabi’s expansion of the ‘ud tuning. Also, in the last quotation of Chapter 10, Section 54, Mersenne acknowledges the importance of embracing new musical intervals, which resembles Al-Farabi’s desire, “ . . . to count as somewhat natural those intervals which are sometimes or rarely regarded as natural.”
More than thirty years ago, I coined the term ambisonance. From the Greek amphi as in amphibian, and the Latin ambi as in ambidextrous, these two prefixes literally mean on both sides. For me, figuratively, they mean partaking of two worlds. Ambisonance describes hearing a musical interval for the first time with the sudden realization that such an interval produces neither a consonance nor a dissonance. Experiences of ambisonance inspire new ways to hear, and then new ways to tune and to compose.
[21]Forster Translation: La Musique Arabe, Volume 1, pp. 49–51.
[22]Forster Translation: La Musique Arabe, Volume 1, pp. 51–52.
In La Musique Arabe, Volume 1, p. 313, D’Erlanger explains why he translated the Arabic word quwwah, — literally “power,” “force,” or “strength,” — with the Greek word dynamis, also “power,” “force,” or “strength.” Furthermore, D’Erlanger arbitrarily interjects the French word puissance — also “power” or “force” — in places where the original Arabic is not given.
In An Annotated Glossary of Arabic Musical Terms, Greenwood Press, Westport, Connecticut, 1981, p. 269, L.I. Al-Faruqi gives the following three definitions for quwwah:
1. The relationship or identity that occurs between two tones one octave apart, i.e., either the upper octave equivalent or the lower octave equivalent of a tone. 2. The term also referred to any tone produced on the ‘ud which had one or more octave equivalent tones within the range of that instrument. Other tones, which had no octave equivalents within the range of the ‘ud were termed mufradah. 3. Tension of a string, therefore pitch.
Note, therefore, that in a musical context, the hierarchical meaning of the word quwwah is octave, then octave equivalent, and finally pitch. Although quwwah may connote the “power,” “force,” or “strength” of an octave, of an octave equivalent, or of a pitch, in the context of tuning descriptions, quwwah specifically refers to ancient length ratio or frequency ratio 2/1, which is the octave of 1/1; similarly, it may refer to ancient length ratio or frequency ratio 9/4, which is the octave equivalent of 9/8; etc. (See Chapter 9, Section 4.)
D’Erlanger gives the following three reasons for using the Greek word dynamis: (1) Dynamis means quwwah because an octave or an octave equivalent acts to give “power,” “force,” or “strength,” to a given lower tone. (2) D’Erlanger states that since the Greeks used dynamis to describe the function of a tone, dynamis also means the “place” or “position” which a given tone occupies in a tetrachord or scale. (3) D’Erlanger claims that because one may express a progression of octaves and octave equivalents through a so-called power series of ratios, as in

there exists a mathematical justification to translate quwwah as dynamis. Finally, consistent with the first and third reasons, D’Erlanger also interjects the French word puissance where the topic under consideration centers on such a “power” series.
I categorically reject D’Erlanger’s use of dynamis and puissance as explained by the first and third reasons. In a musical context, and in the context of tuning descriptions, the Greek word dynamis and the French word puissance do not mean octave or octave equivalent. Since the Arabic word quwwah does mean octave or octave equivalent, I have consistently translated dynamis and puissance as either octave or octave equivalent. For example, in Section 11.59, Ibn Sina’s highly accurate tuning description of two extra tones on the fourth string of the ‘ud does not refer to puissance, but to two octave equivalents, namely, ancient length ratios or frequency ratios 32/9 and 4/1. Readers who, through no fault of their own, fail to understand this sentence as a reference to two highly specific scale degrees will also fail to comprehend the meaning of Ibn Sina’s description. Finally, D’Erlanger’s utilization of dynamis to mean the function or position of a given tone in a tetrachord or scale is correct. However, to minimize confusion and to avoid costly mistakes, a translator should never translate a given foreign language (Arabic) into another foreign language (Greek) that the reader of the translation (French) may not understand.